Timer LLC

Обратная задача и ее решение для георадаров ГРОТ

Физические принципы работы всех георадаров одинаковы. Для получения информации о среде необходимо решить обратную задачу. Решение обратной трехмерной задачи восстановления подповерхностной структуры грунта является крайне сложным из-за потребности в больших вычислительных ресурсах. В то же время именно решение такой задачи в полной постановке, т. е. на основе дискретизации уравнений Максвелла и нахождения устойчивого решения, позволяет автоматизировать процесс интерпретации данных георадарного зондирования.

Обратная задача в георадиолокации — это задача восстановления значений параметров среды из данных георадиозондирования.

Все обратные задачи являются некорректно поставленными задачами, то есть задачами, в которых нарушено хотя бы одно из условий:

• существование решения
• единственность решения
• его устойчивость (условие, при котором решение непрерывно зависит от входных данных, то есть устойчиво по отношению к малым возмущениям данных наблюдений)

Решением прямой задачи является поиск следствия некоторого процесса по его известной причине. Например, можно рассчитать параметры поля при распространении в среде определенного электромагнитного импульса с заданными параметрами этого импульса и среды, в том числе в среде с вкраплениями неоднородностей. Кроме того, решение прямой задачи позволяет рассчитать динамический диапазон прибора для обнаружения тех или иных неоднородностей.

В отличие от решения прямой задачи, решение обратной задачи затруднено тем, что один и тот же эффект может быть порожден разными причинами или какой-либо их совокупностью. Иногда совокупность разных факторов может даже маскировать искомый эффект. Например, при часто встречающихся случаях зондирования водоемов зимой при малой разрешающей способности георадара вместо двух границ (лед-вода и вода-дно), он показывает одну (вода-дно), при этом расстояние до границы вода-дно искажается. При локализации неоднородностей также часто возникают ошибки, связанные с наложением эффектов (например, при локализации труб) вызванных наличием траншей. Следует учитывать и степень когерентности шумов, которые зачастую приводят к появлению ложных объектов при интерпретации, в самих приборах.

До сих пор основой для интерпретации данных в георадиолокации является принцип, по которому расстояние до отражающего объекта определяется по временам запаздывания отраженного сигнала относительно момента излучения зондирующего импульса. При этом амплитуда отраженного сигнала зависит от степени поглощения радиоволн в исследуемой среде и коэффициента отражения на контакте сред. Для описания явления используются законы геометрической оптики. 1

Отметим, что возможность использования такой кинематической модели для решения обратной задачи, основанной на лучевой теории распространения волн и применяемой при интерпретации данных георадара, подходит при использовании относительно коротких длин волн в средах со слабой проводимостью. При увеличении длин волн и в средах с существенной проводимостью лучевую теорию следует применять с осторожностью, а параметры самого георадара должны соответствовать особенностям распространения импульсных сигналов в реальных средах.

При георадарных исследованиях зондирующие сигналы в реальных средах могут иметь характерные времена длительности, сопоставимые с временами проявления механизмов поляризации среды. Изменение не только амплитуды, но и формы сигнала при распространении в реальных средах, приводит к необходимости формирования при конструировании георадара линейной характеристики узлов приемника, использующихся при оцифровке отраженного сигнала. Например, частотное и временное стробирование приводит к дополнительным искажениям сигнала и, следовательно, к ошибкам при интерпретации данных. Заметим, что сами характеристики сигнала при распространении в разных средах зависят от способа их определения. [2,3] Так, эмпирические данные о затухании сигнала на определенной частоте, часто использующиеся для оценки глубин зондирования и залегания неоднородностей, не могут быть с достаточной достоверностью положены в основу анализа предельно возможной глубины исследования, если неизвестны параметры георадара.

Для правильного восстановления параметров среды при качественной и количественной интерпретации данных георадиолокационных измерений необходимо учесть влияние таких параметров георадара, как его мощность, длина и крутизна переднего фронта импульса передатчика, частота и разрядность АЦП, линейность характеристик приемника, а также параметры антенн, влияющие на диапазон частот и дисперсионную зависимость широкополосного импульса.

Решение задачи восстановления по данным георадара подповерхностной структуры грунта должно учитывать большой набор параметров и требует высокого профессионализма интерпретатора. Для получения решения, некорректную задачу нужно доопределить. Для этого необходима дополнительная априорная информация, вытекающая из опыта исследований и экспериментальных материалов. Основываясь на накопленном опыте, исследователь в георадиолокации подбирает наиболее оптимальную упрощающую модель, и в рамках этой модели интерпретируются полученные данные.

Упрощающие модели в георадиолокации

• В георадиолокации применяют различные упрощающие модели, в том числе следующие: Модель, описывающая поле в рамках волнового приближения и оперирующая временами задержки отраженного сигнала для определения структуры исследуемой среды. В этой модели можно воспользоваться накопленными алгоритмами, применяемыми для сейсморазведки: методы деконволюции, преобразования Гилберта и т.д. 1Если данные представимы в рамках этой модели, то интерпретация дает однозначные результаты при зондирующем импульсе треугольной формы непосредственно по радарограммам. Эта модель высокочастотного приближения малоэффективна в средах с высокой проводимостью, что определяет низкую эффективность применения некоторых георадаров для исследования низкоомных сред даже в настоящее время.
• В зависимости от области рабочих частот зондирующего импульса, применяют высокочастотное и низкочастотное приближения при решении уравнений Максвелла, в которых можно использовать модели для коэффициента диэлектрической проницаемости и тем самым упростить уравнения, пренебрегая соответствующими членами. Такой подход является хорошим регуляризующим алгоритмом для получения качественных результатов. При таком подходе, решение весьма упрощается. [2,3]
• Одномерные и двумерные приближения, для которых в некоторых случаях можно выписать аналитические решения и тем самым найти характерные качественные, а иногда и количественные особенности решения.

Использование той или иной модели предполагает высокий профессионализм интерпретатора, поскольку изучаемая нами среда, образ которой представлен данными георадиолокации, разнообразна. При этом неправильный выбор модели задачи приводит к неправильному решению.

Необходимость повышения качества диагностики и идентификации подповерхностных областей и объектов по результатам георадарного сканирования и желание облегчить работу интерпретатора георадиолокационных данных и, в идеале, получать решение задачи автоматически приводят к необходимости решения обратных задач рассеяния в максимально полной трехмерной постановке.

Как известно, обратная задача георадиолокации может быть задана в полной постановке на основе уравнений Максвелла. До сих пор универсальное решение такой задачи не получено, хотя подходов к решению существует довольно много. 4

Общеизвестно, что решение задачи в общей постановке требует больших вычислительных мощностей и большого времени для проведения необходимых вычислений. При этом для георадиолокации весьма существенной потребностью является обработка данных в реальном времени непосредственно в процессе георадарной съемки. Мы сконцентрировали наши усилия именно на решении этих проблем.

Наш подход к решению обратной трехмерной задачи в георадиолокации

Решение уравнение Максвелла для этой задачи строится на адаптивных сетках. Основная сложность решения таких задач заключается в правильной дискретизации уравнений Максвелла на заданных неравномерных сетках и в решении очень плохо обусловленных разреженных систем уравнений с большим количеством неизвестных.

Для решения такой задачи на основе численного моделирования уравнений Максвелла мы предлагаем два вида сеток:

Тензорные сетки

Этот тип сетки позволяет представлять матрицу в задаче наименьших квадратов в виде многоуровневой-блочно-Теплицевой. Это уменьшает арифметические затраты и требования к объему памяти. В то же время, для более точного представления искомого объекта, необходимо сильно измельчать сетку и вводить специальные регуляризаторы, что может качественно ухудшить решение.

Адаптивные многогранники Вороного-Делоне

Используя такие сетки, мы получаем более устойчивое представление об изучаемом объекте. В то же время, неструктурированная сетка требует специальных многоуровневых и иерархических матричных методов, отличных от метода быстрого преобразования Фурье.

Разработанные и успешно применяемые нашими партнерами из фирмы "Elegant Mathematics" LTD уже более 15 лет итерационные методы для решения систем уравнений позволили нам найти наиболее подходящий и устойчивый метод решения линейных систем и, при необходимости, регуляризовать вырожденную матрицу.

Эти алгоритмы использовались суперкомпьютерным центром Мауи (Гавайи, США) по поручению компании Мобил для решения такого типа плохо обусловленных разреженных систем уравнений с регуляризацией с использованием массивно-параллельных компьютеров.

Объем используемой памяти компьютера и время проведения расчетов пропорциональны объему моделируемого объекта и пространственному разрешению сетки. Применение совершенных вычислительных алгоритмов, разработанных в последнее время, дало возможность решать подобные задачи для значительных объемов неизвестных параметров, описывающих восстанавливаемую пространственную структуру с требуемым разрешением сеток.

Алгоритм решения мы сделали достаточно гибким, чтобы была возможность учесть априорную информацию. Так, любая априорная информация может быть использована в качестве регуляризатора.

Сама программа, реализующая наш алгоритм, имеет возможность анализировать промежуточные решения с помощью программ визуализации, прерывать итерации решения и т. д.

Схематично, решение состоит из сравнения измеренного поля на поверхности с вычисленным набором полей, являющихся результатом решения прямой задачи распространения импульса в среде с заданным распределением электромагнитных параметров.

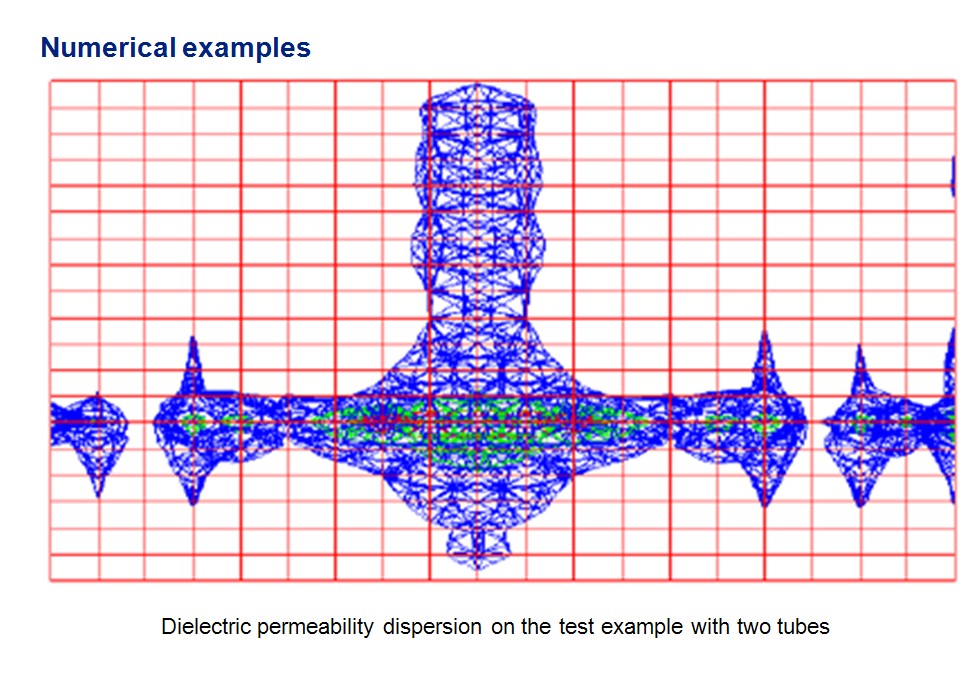
Оценка погрешности может быть проведена для решения прямой задачи с заданным значением узлов сетки. Например, через помещение двух металлических предметов (труб) перпендикулярно друг к другу в однородной среде. Для выбранного диаметра труб, соответствующего двум отсчетам сетки, решение представлено на рисунках в двумерном и трехмерном видах и дает представление о погрешности для данного набора параметров.

В частности, рисунки демонстрируют зависимость точности решения от поляризации антенн. И, соответственно, при планировании эксперимента всегда можно подобрать необходимую технологию съемки для обеспечения необходимой точности результатов. Решение было успешно опробовано для археологических задач.

На рисунке 3 показан пример решения трехмерной обратной задачи поиска расположения неоднородного включения в археологических задачах. Необходимо отметить, что решение в данном случае системы из 10000 неизвестных было получено за несколько секунд машинного времени на обычном персональном компьютере, непосредственно на месте проведения съемки. Этот пример был выбран для наглядности, т. к. после проведенного георадарного сканирования на этом участке были проведены раскопки, и было подтверждено, что данные решения обратной задачи имели точность до 10 см. Усложнение задачи из-за увеличения объема изучаемого объекта и, следовательно, увеличения числа неизвестных в обратной задаче, к примеру, до 1000000 приводит к увеличению времени счета до 1 часа. Таким образом, задача восстановления трехмерной структуры исследуемых площадок становится доступной для решения непосредственно в полевых условиях.

На этом рисунке представлен 3D-образ исследуемой среды в программе Grot12.

В заключение отметим, что наш подход к решению обратной трехмерной задачи в георадиолокации позволяет нам с помощью георадаров ГРОТ успешно решать самые сложные задачи в реальном времени, что было подтверждено многочисленными экспериментами.

Литература:

1. Владов М. Л., Старовойтов А. В. Георадиолокационные исследования верхней части разреза М. МГУ, 1999, 92 с.

2. E. A. Rudenchik, L. B. Volkomirskaya and A. E. Reznikov Investigation of the Propagation of Signals in One-Dimensional Electrodynamics for interpretation Electromagnetic Sounding Data. Consideration of the Analytic Properties of Permittivity, Physics of Wave Phenomena, 2008, Vol. 16, No. 1, pp. 1-18. © Allerton Press Inc., 2008.

3. E. A. Rudenchik, L. B. Volkomirskaya and A. E. Reznikov Investigation of the Propagation of Signals in One-Dimensional Electrodynamics for interpretation Electromagnetic Sounding Data Consideration of Conductivity in the Function of Permittivity, Physics of Wave Phenomena, 2008, Vol. 16, No. 2, pp. 1-14. © Allerton Press Inc., 2008.

4. Вопросы подповерхностной радиолокации, под ред. Д. т. н. А. Ю. Гринева, Радиотехника, Москва, 2005г., 416 с.

5. Ибрагимов И. В., Ибрагимова Е. И., Волкомирская Л. Б., Резников А. Е. Международная Конференция по Математическим Методам в Геофизике «ММГ-2008» Россия, Новосибирск, Академгородок, 13-15 октября 2008 г., ММГ 2008

6. L. Volkomirskaja, A. Reznikov, I. Ibragimow and E. Ibragimowa, Investigation with GROT 12 3D Radars and Real Time Solution of 3D Ground-Penetrating Inverse Problem. GPR2008, Birminghem, 15-19 July 2008

7. Волкомирская Л. Б., Ибрагимов И. В., Ибрагимова Е. И., Варенков В. В., Сахтеров В. И., Резников А. Е., Руденчик Е. А. Решение трехмерной обратной задачи георадиолокации по данным георадара ГРОТ 12 , " ИНЖГЕО-2008" , 4-я международная научно-практическая конференция по инженерной и рудной геофизике, 25-30 апреля 2008г., г. Геленджик